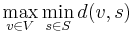Metric k-center

In graph theory, the metric k-center, is a combinatorial optimization problem studied in theoretical computer science. Given n cities with specified distances, one wants to build k warehouses in different cities and minimize the distance of the farthest city from its closest warehouse. In graph theory this means finding a set of k vertices for which the largest distance of any point to its closest vertex in the k-set is minimum. The vertices must be in a metric space, or in other words a complete graph that satisfies the triangle inequality.

1 Formal definition
2 Computational complexity
3 Approximations
4 See also
5 Notes
6 References

Formal definition

Given a complete undirected graph G = (V, E) with distances d(v_i, v_j) ∈ N satisfying the triangle inequality, find a subset S ⊆ V with |S| = k while minimizing:

$\max_{v \in V} \min_{s \in S} d(v,s)$

Computational complexity

If we sort the edges in nondecreasing order of the distances: d(e₁) ≤ d(e₂) ≤ … ≤ d(e_m) and let G_i = (V_i, E_i), where E_i = {e₁, e₂, …, e_i}. The k-center problem is equivalent to finding the smallest index i such that G_i has a dominating set of size at most k.^[1] Dominating set is NP-complete and therefore the k-center problem is also NP-complete.

Approximations

A simple greedy approximation algorithm that achieves an approximation factor of 2 builds S in k iterations. The first iteration chooses an arbitrary vertex and adds it to S. Each subsequent iteration chooses a vertex v for which d(S, v) is maximized and adds v to S. The running time of the algorithm is O(nk).^[2]

Another algorithm with the same approximation factor takes advantage of the fact that the k-center problem is equivalent to finding the smallest index i such that G_i has a dominating set of size at most k and computes a maximal independent set on the of G_i, looking for the smallest index i that has a maximal independent set with a size of at least k.^[3]

It is not possible to find an approximation algorithm with an approximation factor of 2 − ε for any ε > 0.^[4] Furthermore, the distances of all edges in G must satisfy the triangle inequality if the k-center problem is to be approximated unless P = NP.^[5]

Notes

^ Vazirani 2003, pp. 47–48.
^ Gonzalez 1985, pp. 293–306.
^ Hochbaum & Shmoys 1986, pp. 533–550.
^ Hochbaum 1997, pp. 346–398.
^ Crescenzi et al. 2000.

References

Vazirani, Vijay V. (2003), Approximation Algorithms, Berlin: Springer, ISBN 3540653678
Gonzalez, Teofilo F. (1985), "Clustering to minimize the maximum intercluster distance", Theoretical Computer Science, 38, Elsevier Science B.V., pp. 293–306, doi:10.1016/0304-3975(85)90224-5
Hochbaum, Dorit S.; Shmoys, David B. (1986), "A unified approach to approximation algorithms for bottleneck problems", Journal of the ACM (JACM), 33, pp. 533–550, ISSN 0004-5411
Hochbaum, Dorit S. (1997), Approximation Algorithms for NP-Hard problems, Boston: PWS Publishing Company, pp. 346–398, ISBN 0-534-94968-1
Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek; Woeginger, Gerhard (2000), "Minimum k-center", A Compendium of NP Optimization Problems, http://www.csc.kth.se/~viggo/wwwcompendium/node128.html